Studying the Effect of Elastoviscoplastic Modeling on Burst Speed Margins of Turbine Disc

Abstract

Aero engine turbine discs are critical components that can shatter owing to excessive mechanical loads during operation, endangering aircraft safety. Understanding burst speed margins, the buffer between maximum and actual rotational speeds, is essential for ensuring safety. ANSYS APDL software is used to examine a 2D axisymmetric non-uniform turbine disc utilizing INCONEL 718 and Ti-6Al-4V materials and numerous models. This research, which includes centrifugal, gas, and thermal loads, accurately predicts burst speed and confirms linear elastic analysis. For elastic-plastic analysis, Robinson\'s criterion is utilized, Perzyna for elastoviscoplastic behavior, and Bilinear isotropic hardening for elastic-plastic behavior. A sensitivity analysis of Perzyna model parameters reveals that elastoviscoplastic analysis yields higher burst margins than elastic-plastic analysis for this turbine disc. The parameters are calibrated using existing models from the Literature.

Introduction

I. INTRODUCTION

Turbines hold a pivotal role in the field of engineering and power generation by harnessing energy from diverse sources and converting it into valuable mechanical work. These versatile machines find application in a wide array of settings, from powering industrial processes to propelling aircraft. At the heart of these turbines lie the turbine discs, meticulously engineered components designed to bear the brunt of immense mechanical loads and formidable rotational forces. The turbine disc used in the turbojet engines is shown in the figure.

Yet, amidst the impressive functionality of turbines, a lurking peril emerges in the form of overspeed – a scenario in which the turbine's rotational velocity exceeds its meticulously prescribed operational limits. Overspeed, if left unchecked, can unleash catastrophic consequences, none more ominous than the dreaded "turbine disc overspeed burst."

This burst constitutes a grave and potentially hazardous eventuality, characterized by the turbine disc's rotational speed breaching its maximum safe operational threshold. A multitude of factors, ranging from abrupt load variations to control system anomalies and mechanical irregularities, can conspire to push the turbine disc into this treacherous territory.

The aftermath of a turbine disc overspeed burst paints a grim picture. The relentless rotational forces exerted upon the disc can propel it past the limits of its material strength, resulting in mechanical failure of dire proportions. In the wake of such a burst, the disc may fissure, rupture, or fragment, imperiling not only the integrity of the turbine itself but also posing a formidable risk to surrounding equipment and the safety of personnel. To mitigate the looming specter of turbine disc overspeed bursts and ensure a climate of secure and dependable operation, meticulous turbine design and comprehensive analysis are imperative. Engineers wield an arsenal of finite element tools (FEA) to dissect the behavior and vulnerabilities of these critical components, enhancing their understanding and predictive capabilities. The gravity of turbine disc failure extends beyond safety considerations; it exacts a significant toll on the economic landscape. Consequently, the imperative to comprehend, predict, and mitigate the risks associated with turbine disc overspeed bursts transcends engineering pursuit, emerging as a safeguard against both perils and financial repercussions. Depending primarily on elastic-plastic analysis falls short of the mark in the search of precise and dependable burst speed assessment for turbine discs. To provide a full assessment of burst speeds, elastoviscoplastic analysis must be performed. This more complex methodology not only improves our understanding but also our capacity to foresee and anticipate crucial failure sites, assuring the highest level of safety and integrity in turbine operations.

II. LITERATURE REVIEW

Researchers and engineers have worked hard over the years to examine the burst speed margin of elastic, elastic-plastic, and elastoviscoplastic turbine discs. Numerous studies have investigated various theoretical, experimental, and computational techniques for precisely and effectively assessing the burst speed margin.

A series of studies in the field of turbine disc research have provided useful insights into overspeed burst analysis. Mazière et al. [1] used experimental and finite element approaches to explore spinning disk overspeed bursts, and found significant agreement between numerical and experimental results. In later work [2,] they investigated elastoviscoplastic rotating disks, emphasizing the impact of material characteristics on disk stability, notably the significance of material viscosity.

Ranjan Kumar et al. [3] assessed the burst margin of gas turbine discs using finite element modeling, indicating the sensitivity of the burst margin to rotational speeds and the benefits of variable thickness discs. Nicola Squarcella et al. [4] demonstrated the greater accuracy of Robinson's semi-empirical technique over finite element analysis for burst speed prediction.

Maruthi B.H. et al. [5] concentrated on aero-engine discs, using finite element modelling to estimate overspeed and burst margin limitations at different temperatures, emphasizing the importance of tangential stress components in changeable temperature scenarios.

Hojjati et al. [6] investigated non-uniform thickness and density rotating discs and found that the VMP approach and finite element analysis findings agreed quite well. Lakshman Kasina et al. [7] carried out a computational study to estimate stresses and optimize turbine disc designs for weight reduction. Their findings highlighted the significance of bore width, bore radius, bore height, web width, and neck width in shaping burst margins and disc stress distributions. These research, taken together, add to our understanding of turbine disc behavior and safety.

A.K. Asraff et al. [8] investigated the viscoplastic characteristics of high-temperature Austenitic Stainless Steel. Using an INSTRON 8862 electromechanical UTM, they calibrated the Perzyna model parameters via tension tests and the Chaboche and Voce model parameters using low-cycle fatigue testing at 1000 K. The Perzyna model parameters were validated by comparing tension test results to finite element simulations performed with ANSYS (Version 16.0) software. They also performed a viscoplastic cycle stress analysis on a double-walled rocket engine thrust chamber, demonstrating the material's higher dynamic yield strength due to strain rate effects in both experimental and numerical data. A combination of Perzyna and the MISO model produced positive results when modelling monotonic loads. The Perzyna model, in conjunction with Chaboche's nonlinear kinematic hardening model and Voce's nonlinear isotropic hardening model, proved extremely effective in cyclic loading scenarios. The researchers also investigated the sensitivity of Perzyna model parameters'm' and 'D,' discovering that decreasing these parameters intensified rate-dependent effects.

III. SCOPE OF THE STUDY

The study's main goal is to compare the burst speeds obtained from elastic-plastic and elastoviscoplastic analysis of a 2D axisymmetric turbine disc subjected to complex loading (gas, thermal, and centrifugal loading) using a finite element tool, and to show the accurate results of the burst margins. Also, conduct a sensitivity analysis on the influence of Perzyna model parameters on burst margins.

A. Parametric Model

The geometry of the turbine disc model was obtained from the public domain. For the modeling, a turbine disk model generated from a turbine assembly of a legacy engine is used. The figure depicts the geometry of the turbine disc.

a. Sensitivity Study on ‘m’

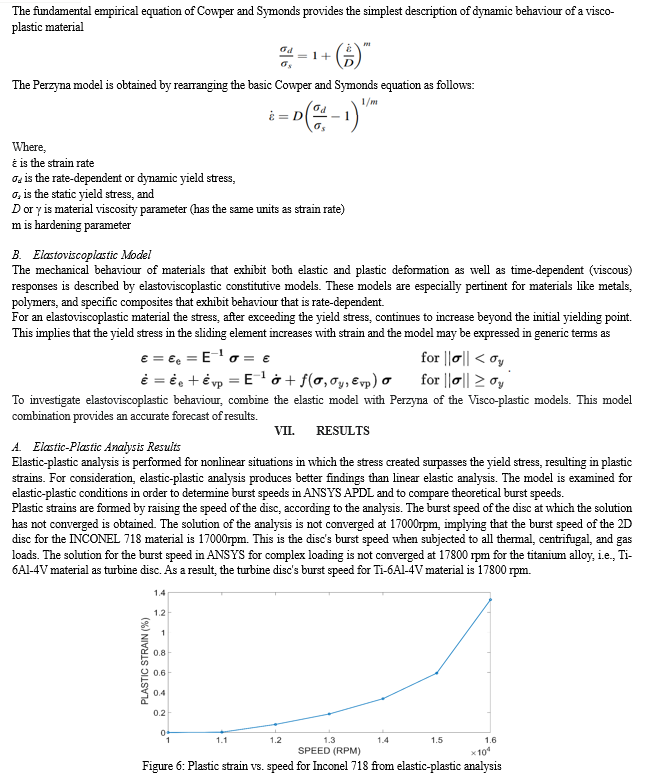
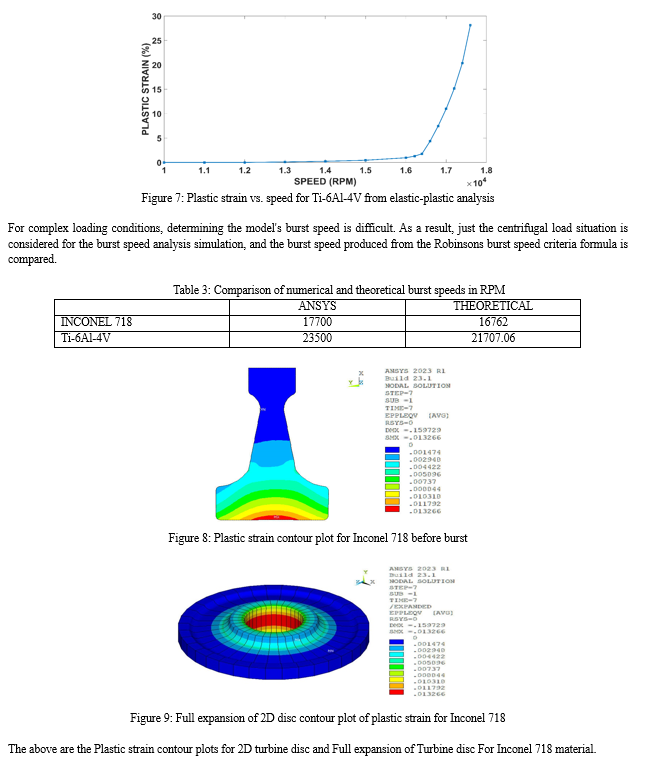
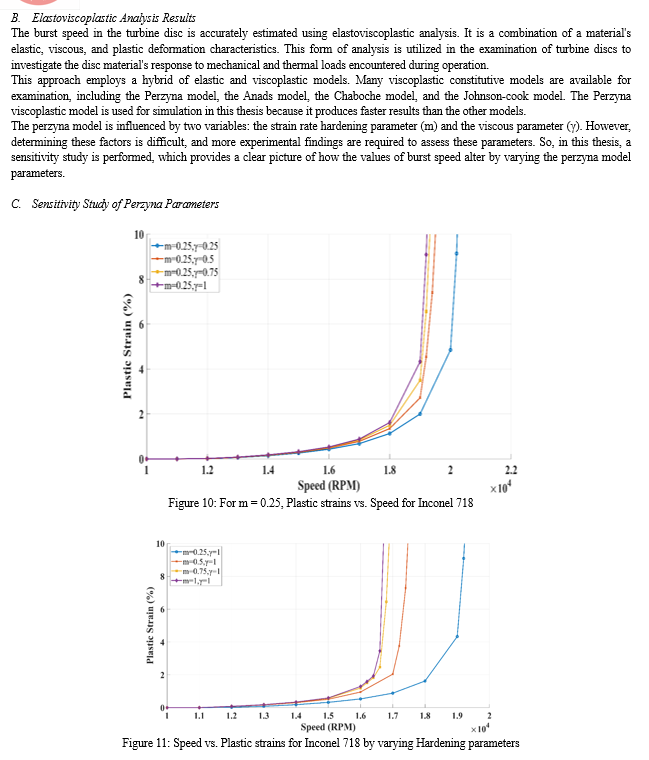
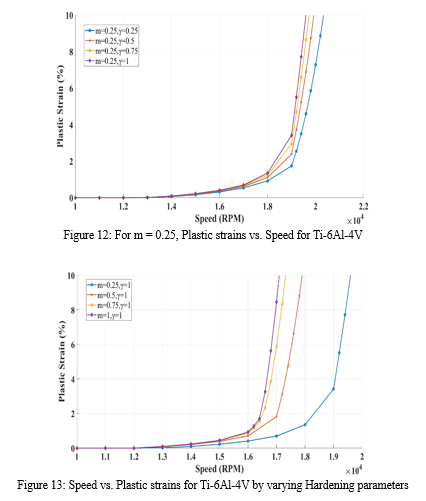
The hardening parameter (m) sensitivity analysis is performed on Inconel718 and Ti-6Al-4V alloys. The graphs show that increasing the hardening parameter 'm' increases the plastic strains while keeping the viscous parameters constant. When compared to the viscous parameter 'm,' which has the greatest influence on material behaviour. This parameter has an effect on the burst margins as well. The burst margin grows as the hardening value is reduced from 1 to 0.25.

b. Sensitivity Study on ‘γ’

The viscous parameter ‘γ’ is the material property. When the viscosity parameter is increased, the material becomes more viscous and rate-sensitive. This means that the material will deform and respond more slowly under applied loads. However, based on our data, the hardness parameter has a greater impact than the viscous parameter. That is why plastic strains grow as the viscosity parameter increases. As ‘γ’ increases from 0.25 to 1, the burst speed margin decreases.

In this work, the burst speeds are estimated using the Perzyna model by adjusting the sensitivity parameters, and the burst speeds vary for different parameters. The hardening and viscous parameters are essential for obtaining accurate results. However, determining these characteristics is quite challenging. It is recommended to conduct experiments on the material to obtain the correct parameters for determining accurate burst speeds.

D. Comparison between Elastic-plastic and Elastoviscoplastic analysis

The burst speeds are obtained for Inconel 718 and Ti-6Al-4V materials using Elastic-plastic and Elastoviscoplastic analysis in ANSYS APDL.

Table 4: Summary of results

According to the table, the burst speeds from the elastoviscoplastic analysis are greater than those from the elastic-plastic analysis for both materials, Inconel 718 and Ti-6Al-4V. As in the case of aero engines, disc failure is catastrophic, and elastic-plastic analysis is sufficient for the study. However, Elastoviscoplastic analysis is recommended for precise estimation of the burst speed margins of the turbine discs.

E. Calibration with Perzyna Parameters from Literature

The perzyna model parameters are extremely difficult to determine. Furthermore, more experimental investigations on the material utilized for the disc at various working circumstances and loading rates are required. A.K. Asraff et al. [11] conducted research on the evaluation of the visco-plastic parameters of an austenitic stainless steel at high temperatures and published data on the calibration of Perzyna model parameters of an austenitic stainless steel from tension testing. A clear approach for determining the perzyna model parameters is described in that literature. By conducting experimental tensile tests on SS-321 material, the parameters hardening parameter 0.412 and viscous parameter 0.322 were acquired from the approach.

These characteristics are taken into account for the turbine disc in this thesis for validation.

The elastic-plastic parameters yield a burst speed of 8000 rpm, whereas the elastoviscoplastic parameters yield a burst speed of 11000 rpm. As a result, the parameters chosen are validated since elastoviscoplastic analysis predicts burst speed greater than elastic-plastic analysis. Therefore, the parameters generated in the literature are then used for the Inconel 718 and         Ti-6Al-4V materials of the 2D disc.

Using the perzyna model parameters, the Inconel 718 material model bursts at 22000 rpm, while the Ti-6Al-4V material model bursts at 25000 rpm. When these burst speed margins are compared to elastic-plastic analyses, these burst speeds are greater. This investigation concludes that elastoviscoplastic analysis provides higher burst speeds than elastic-plastic analysis. However, calibration of the sensitivity parameters is more important for accurate results.

VIII. ACKNOWLEDGMENTS

The author is grateful to the management and leadership of Cyient Ltd for their important input and technical assistance.

Conclusion

From this in-depth analysis of turbine disc failure behaviour, several significant conclusions can be drawn. These conclusions shed light on the factors contributing to turbine disc failures and provide valuable insights for enhancing the reliability and performance of turbine systems. Through meticulous examination and interpretation of the data, a clearer understanding of the failure mechanisms has emerged, paving the way for informed strategies to mitigate such failures in the future. 1) The nickel-based alloy Inconel 718 and the titanium alloy Ti-6Al-4V materials are utilized for the turbine disc material, and the burst speed margins vary due to differences in densities. 2) The burst speeds predicted from the Robinson\'s criterion of failure of the turbine disc are quite close to the findings obtained from ANSYS by considering only centrifugal loading because evaluating complex loading for elastic plastic conditions is difficult. 3) Sensitivity analysis is performed for the Perzyna constitutive model parameters in order to gain a better understanding of the Viscoplastic behavior of the turbine disc model, and it is concluded that the Perzyna model parameters have a greater impact on the analysis of burst margins and the increase of hardening parameter, which increases the plastic strains. 4) According to this thesis, the burst speeds obtained from the elastoviscoplastic analysis provide higher burst margins than the elastic-plastic analysis of the turbine disc subjected to centrifugal loading + thermal loading and gas loadings using numerical software.

References

[1] Mazièr,M., Besson, J., Foresta, S., Tanguy, B., Chalons, H., Vogelb, F., 2009, “Overspeed Burst of Elastoviscoplastic Rotating Disks: Part II – Burst of a Superalloy Turbine Disk”, European Journal of Mechanics A/Solids 28 (2009) 428–432. [2] Mazièr,M., Besson, J., Foresta, S., Tanguy, B., Chalons, H., Vogelb, F., 2008, “Overspeed burst of elastoviscoplastic rotating disks – Part I: Analytical and numerical stability analyses.” European Journal of Mechanics A/Solids 28 (2009) 36–44. [3] Ranjan Kumar., Vinayak Ranjan., Bipin Kumar., 2017, “Finite element modelling and analysis of the burst margin of a gas turbine disc using an area weighted mean hoop stress method.” Engineering failure analysis, S1350-6307(16)30700-2. [4] Nicola Squarcella., Christian Maria Firrone., Marco Allara., Muzio Gola., 2014, “The importance of the material properties on the burst speed of turbine disks for aeronautical applications.” International Journal of Mechanical Sciences 84 (2014) 73–8. [5] Maruthi B H., M. Venkatarama Reddy., K. Channakeshavalu., 2012, “Finite Element Formulation for Prediction of Over-speed and burst-margin limits in Aero-engine disc.” International Journal of Soft Computing and Engineering (IJSCE) ISSN: 2231-2307, Volume-2, Issue-3, July 2012. [6] M.H. Hojjati., A.Hassani., 2008, “Theoretical and numerical analysis of rotating discs of non-uniform thickness and density.” International journal of pressure vessels and piping 85(2008) 694-700. [7] Lakshman Kasina., Raghavan Kotur., Govindaraji Gnanasundaram., 2015, “Minimum Weight Design of Aero Engine Turbine Disks.” ASME, GTINDIA2015. [8] A.K. Asraff., Merin V. George., Krishnajith Jayamani and S. Sarath Chandran Nair., 2018, “Evaluation of Visco-plastic Parameters of an Austenitic Stainless Steel at High Temperature.” Fatigue, Durability and Fracture Mechanics. [9] Chianese Stefano, Master thesis

Copyright

Copyright © 2024 Bheesetti Haresh Swamy, Putti Srinivasarao, H. Leela Kishore, Lakshman Kasina. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.